Abstract¶
A brief overview of matrices, operations of matrices and other key properties.
Matrix Definition¶
Let be some integers. An matrix over a field is a rectangular array of numbers with rows and columns, such that
The values are called the matrix elements of .
If , the matrix is called a square matrix.
The th row of is given by
and the th column is given by
which can be thought of as row and column vectors respectively. The set of matrices over the field is given by .
Matrix Operations:¶
Let , , .
The transpose of , given by , is the matrix obtained by swapping the roles and columns of the matrix . If the matrix element of in the th row and th column is given by , the matrix elements of in the th row and th column is given by .
Properties:
.
Let , .
The conjugate transpose of , given by , is the matrix obtained by first transposing , given by , and then taking the complex conjugate of all its elements, given by . This operations can be done is any order, such that .
Properties:
.
Let .
The matrix is invertible (non-singular) if there exists a matrix such that
where is the identity matrix.
Properties
If for some then .
If both and are invertible the is invertible with .
Let and and
The elements is given by
which is the dot product between the th row of A and th column of B. Elements Form.
Note the columns of must equal the rows of for matrix multiplication to be a valid operation. The output matrix is then a matrix, . See the below figure for details.
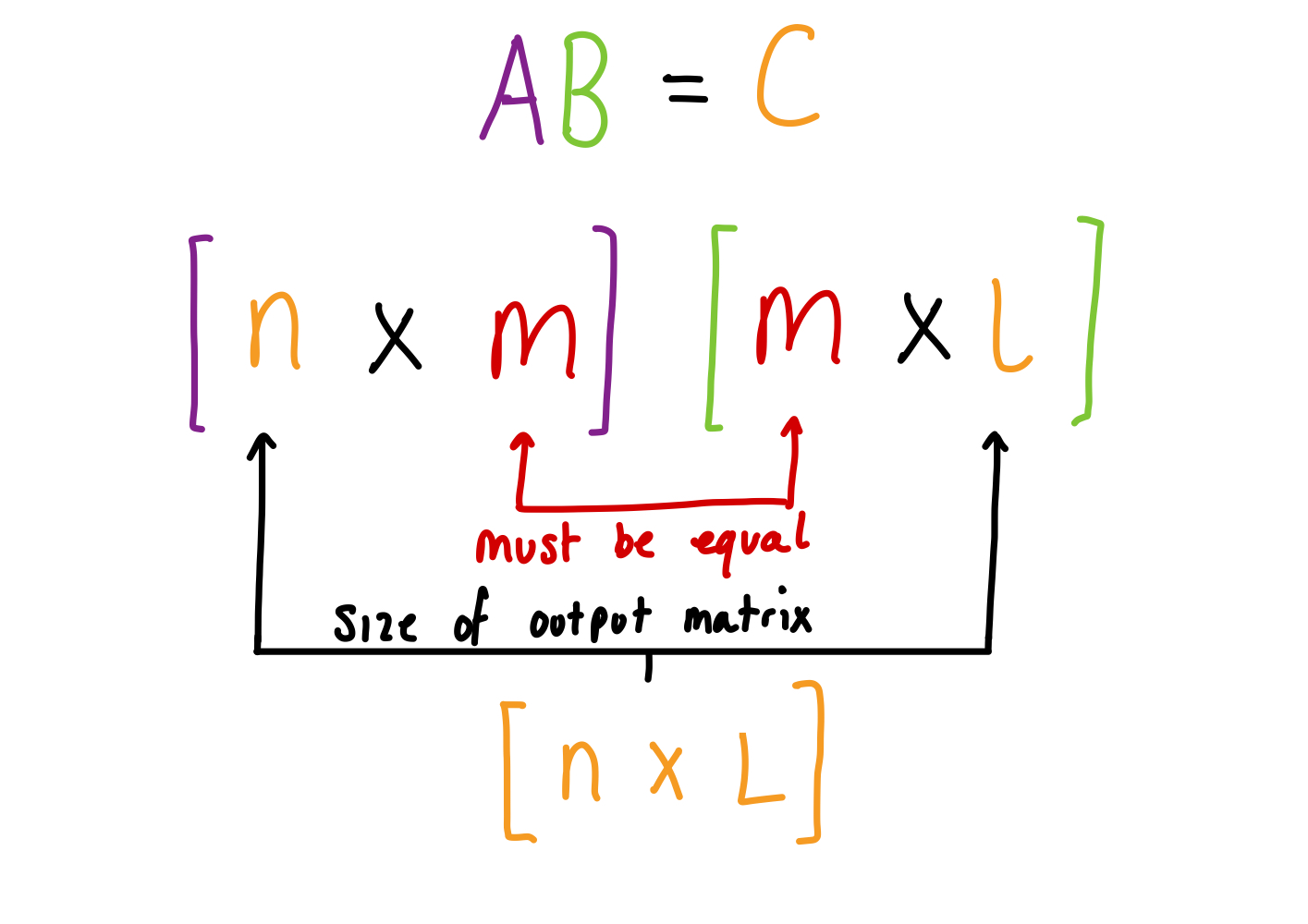
The conditions on a matrix and for them to be compatible for matrix multiplication. The size of the output matrix from the multiplication is shown arising from the size of the input matrices.
Properties:
in general
Let such that , where 0 is the zero matrix
such that , meaning two non-zero matrices can be multiplied to give the zero matrix. Likewise, such that for certain .
Let and
Let and
Let , and
Elements Form
Matrix Properties¶
Let with elements (th row and th column)
is upper triangular if if . For example
is lower triangular if if . For example
Let .
A is symmetric if where is the transpose operation.
Let with elements (th row and th column)
is diagonal if if .
Let with elements (th row and th column)
is positive definite if for all column vectors ,
where is the conjugate transpose operation.
is positive semi-definite if for all column vectors ,
Negative and negative semi-definite are defined the say way but with inequalities in the opposite direction.
A matrix is positive definite if it is both hermitian and has all positive eigenvalue - just having positive eigenvalues if not enough for a matrix to be positive definite or positive semi-definite.