Lines Between Points¶
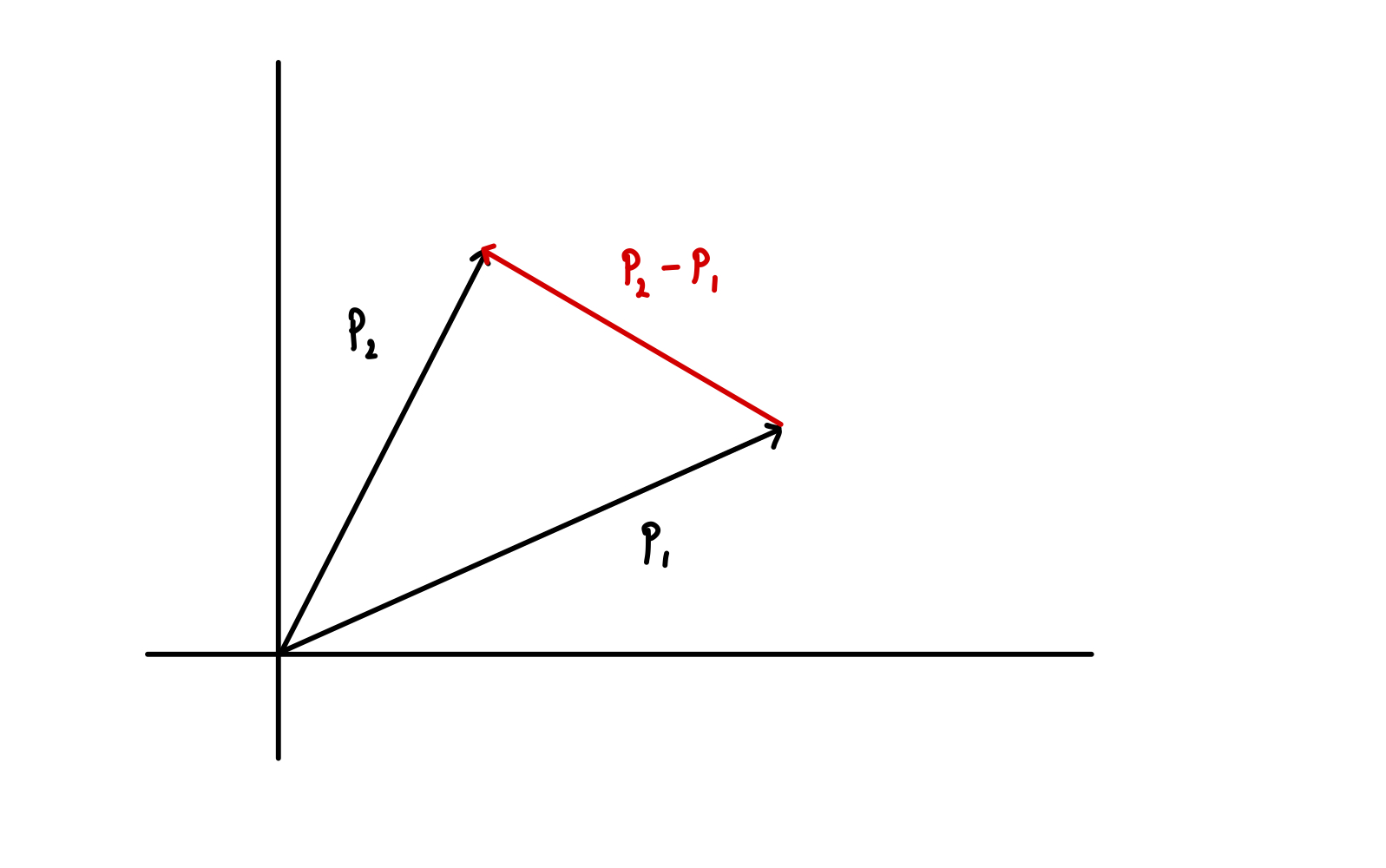
Two vectors, and , drawn with respect to some basis, and the vector that joins them.
The above figure shows two vectors, and drawn with respect to some basis, and the vector, , that joins them. Any point along the line that encompasses the vector can be given by a vector
where is a scalar. If then can be considered to be a probabilistic mixture of the vectors and .
Convex Functions¶
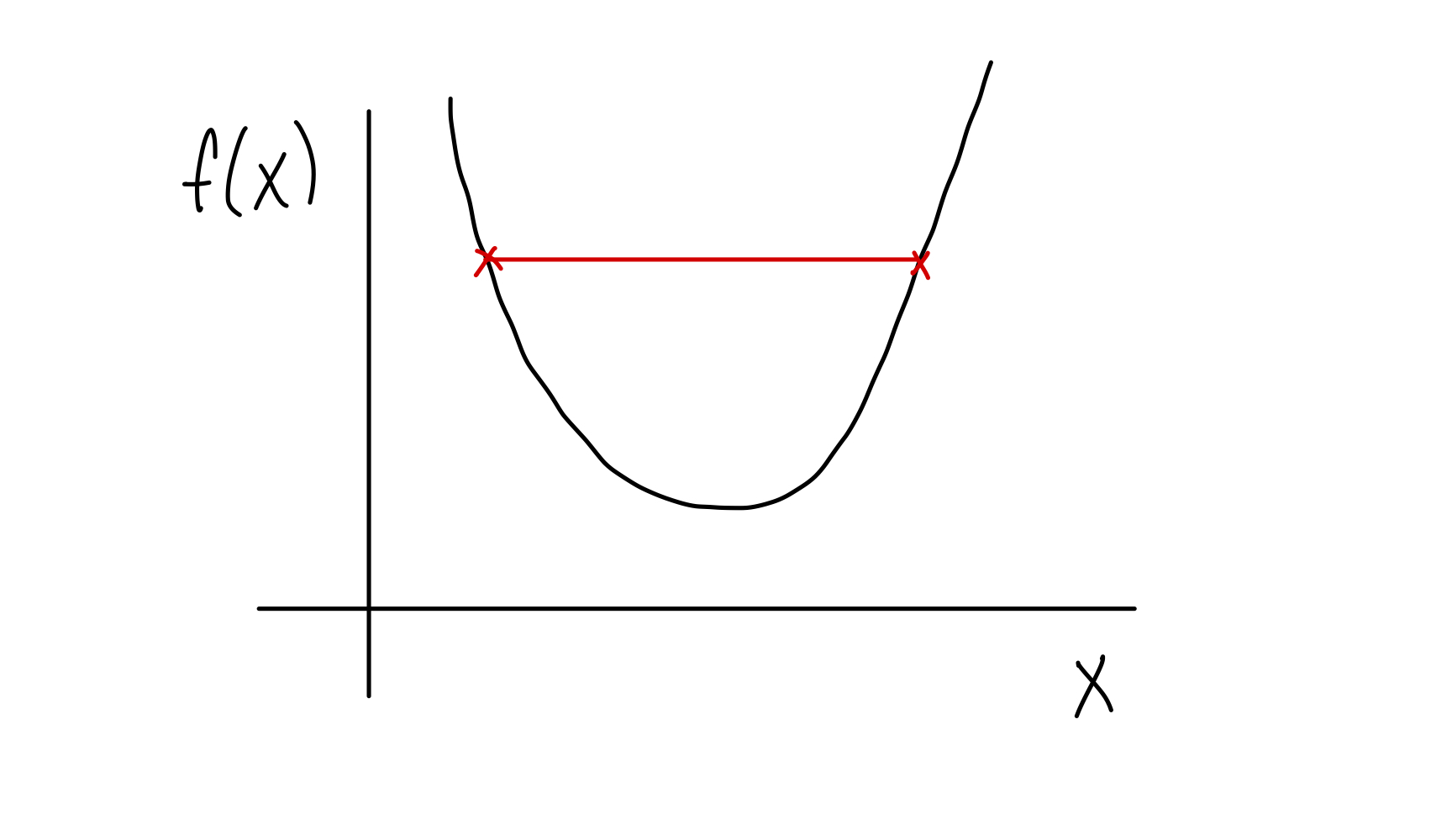
A convex function, .
In the above figure, a function is plotted. For any two points on the graph, and , it can be seen that the value is less then and if . This means all points between and sit below the line-segment between those points. This can be stated mathematically as
The argument of the left hand side, , is the straight line between and . The right hand side is the straight line between and .
If the above criteria is satisfied, the function is a convex function.
Convex Sets¶
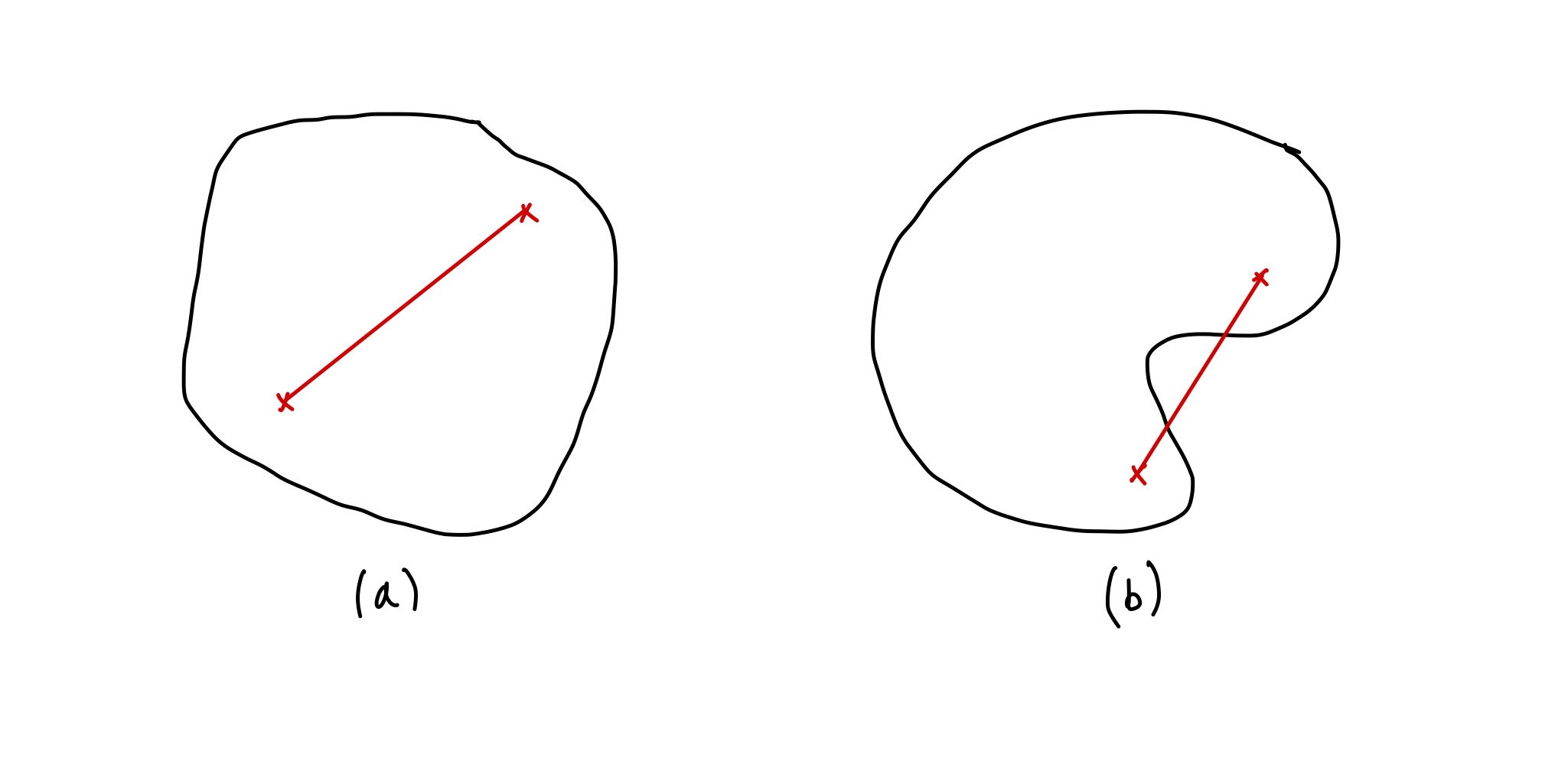
a) A convex set b) a non-convex set.
Let be a vector space over a field . A subset is convex if for all the line segment connecting and is also in , as seen in Fig (a) above. Mathematically this means that
If a mixture of elements in the subset can lead to an element outside of the subset, as seen in fig (b) above where some points on the line segment are outside the boundary of the set, the subset is not convex.
In general, a set is convex if for all subsets of objects in , , then
The boundary of a convex set is always a convex curve.
The convex hull of a set is the smallest convex set that contains .
Affine¶
Let be a vector space over a field . A subset is affine if for every pair in the set the whole infinite line through those two points is in . Mathematically, this means that
The key difference between affine sets and convex sets is that does not need to be in the set and can be negative. This means that the whole line including and is included, not just the line segment between and .
In general, a set is affine if for all subsets of objects in , , then
where, as before, the condition for to be positive has been removed.
Hence, convex combinations can be thought of as a weighted average of elements of the set, whilst affine combinations can be thought of as a weighted average where the weights can be negative.