Abstract¶
Measurements in quantum mechanics can be generalised beyond observables through the notion of generalised measurements and POVMs.
Generalised Measurements¶
This section of notes is partly based on content from Chapter 3 of Resource of the Quantum world
Definition¶
A generalised measurement is a set of operators, , such that
This condition ensures that the sum of the probabilities of getting the different possible outcomes of the measurement is one.
Measuring a Generalised Measurement¶
Let be some quantum state.
When the generalised measurement defined by is applied to the state the post measurement state upon getting the outcome , denoted , is
where is the probability of getting the outcome , given by
If instead one considers a state .
When the generalised measurement defined by is applied to the state , the post measurement state upon getting the outcome , denoted , is
where is the probability of getting the outcome , given by
Physical Realisation¶
All generalised measurements can always be produced from the action of a joint unitary on a state and ancilla, followed by a projective measurement on the ancilla. The measurement outcome is given by the output of the projective measurement on the ancilla. Depending on this output, it is then known what the post measurement state is.
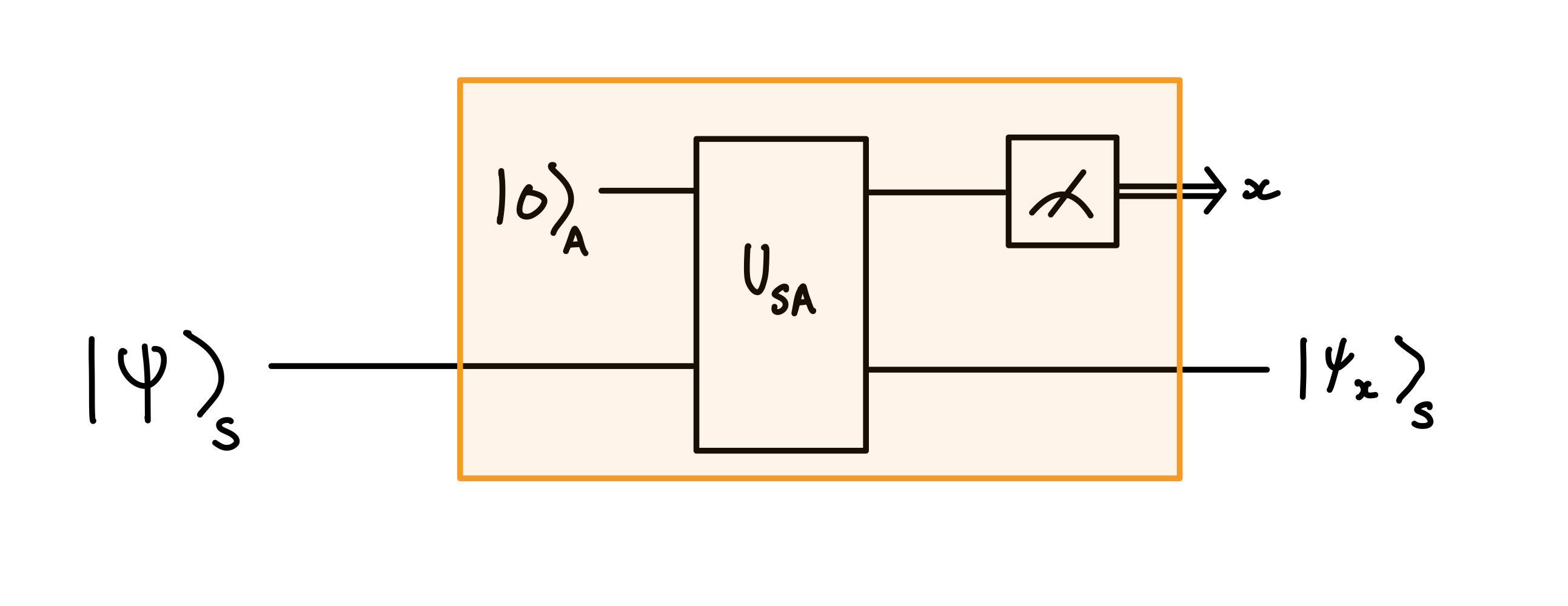
The orange box represents the generalised measurement. A state, first has an ancilla, , appended. A joint unitary, , is then applied on the system and ancilla. A projective measurement is then applied on . The outcome of this measurement then informs the post measurement state in .
Generalised Measurements as a Channel¶
It can be seen from the definition of a generalised measurement that it is the same definition as the Kraus decomposition of a quantum channel - a completely positive trace-preserving map.
Each element of the generalised measurements, , can then be thought to define a completely positive trace non-increasing map on a state. Given a state , the post measurement state is now defined as
where is a completely positive trace non-increasing map. The sum over all these completely positive trace non-increasing maps will then give a completely positive trace preserving map,
due to the definition of a generalised measurement.
In the literature, this is referred to as a quantum instrument. Physically, this says that a generalised measurement performed on a state maps the state to a quantum-classical register where the measurement outcomes are stored in the classical register and the post measurement state in the quantum register. If an outcome is in the classical register, then is in the quantum register. A quantum instrument, , is then defined as the map
POVMs¶
A Positive Operator Valued Measure (POVM) is a generalised measurement where one does not care about the post measurement state, only the probability of getting different outcomes. This might be the case because the post measurement states is unimportant for any future use, or, it might be because it physically does not exists, such as when a photon is measured. In this case, the photon is destroyed, leaving no photon for a post measurement state to exist in.
Hence, rather than considering the set of operators , one can instead consider only the set which is enough to give the probabilities of the different possible outcomes occurring. However, one loses the ability to calculate the post measurement state.
Definition¶
A POVM is a set of operators, , such that
The first condition carries from the definition of the generalised measurement and it once again ensures that the sum of the probabilities of getting the different possible outcomes is one. The second condition ensures that all these probabilities are positive.
Physical Realisation¶
All POVM’s can be physically realised by just performing the associated generalised measurement and ignoring the post measurement state.
Naimark’s dilation theorem
Naimark’s dilation theorem states that every POVM can be realised by a projective measurement (the measurement of some observable) on a higher dimensional space.
Consider a POVM, , acting on a Hilbert space given by
Then there exists a projective measurement
acting on a Hilbert space , where , such that
where , is an isometry.
This theorem ensures that all POVMs are physically realisable through the measurement of an observable on a higher dimensional space.
Properties¶
For each generalised measurement there is a unique POVM that corresponds to it. On the other hand, for each POVM there are many possible generalised measurements that correspond to it.
- Gour, G. (2024). Resources of the Quantum World. arXiv. 10.48550/ARXIV.2402.05474